
Using R, irregular points can be converted to a grid using raster’s rasterize function.
#INTERPOLATE NUMPY RASTER X Y Z CODE#
What if multiple points fall within the area of a raster cell? R Code Now you need to consider methods specifically dealing with this, including the conversion of your points to regularly gridded data, which will require averaging or some sort of function.
Often, your data won’t be regularly spaced. a geotiff), you need to make use of the gdal python bindings. To output the numpy array to a raster (e.g. A flipped array looks like the below (the numpy indices have been left on though to illustrate numpy’s top left origin). This is why the values on the plot above are flipped compared to the earlier scatter of the input points. NB/ Remember that Python considers the grid origin to be the top left corner - if -800 (x) and -3400 (y) were actually the bottom left corner of the grid, you would want to flip the resultant grid i.e. Also, if the exact properties of the RasterLayer are known beforehand, it may be preferable to simply create a new RasterLayer with the raster function instead, compute cell numbers and assign the values with these.Īrray (,, ]) NB/ If using the function and not specifying the raster resolution, it is assumed to be the minimum distance between x and y coordinates. R’s raster package provides functionality to create a raster from regularly gridded points rasterFromXYZ. Where you data are regularly gridded, you can take each point value and associate it directly with a grid cell. In the latter case, where data are not available, a grid cell will not have a value. Note that there is a difference between interpolating a surface from points – interpolating values at locations where observations are not available – and creating a gridded representation of a point dataset. This process can be carried out using various tools (python, gdal etc.) but I find the most succinct approach is to use the excellent libraries from R, namely raster and sp. The formula to interpolate between x1 and x2 is (1 - t) x1 + t x2 where t ranges from 0 to 1. Unless you have all of the information regarding how a DEM was created (including estimates of uncertainty), you can only be truly confident in the values of a DEM if you do the point to raster conversion yourself. Different approaches are taken to convert these points to a DEM raster. every 10 m along north and east directions) or irregularly spaced (i.e. When working with a DEM, it is important to be aware that the values of a given cell are the result of some processing step that converted point elevations to a value at that location. Z = np.DEMs (raster format) are created from point elevation observations. # I'm fairly sure there's a more efficient way of doing this. But if it is, you can avoid having to interpolate: def method_3(): In general, with sampled data, this will not be true.

For every possible unique (x,y) pair, there is a corresponding (x,y,z) in your data.įrom this, it follows that the number of (x,y,z) pairs must be equal to the square of the number of unique x points (where the number of unique x positions equals the number of unique y positions).The length of y along the interpolation axis must be equal to the length of x. y(,N,) arraylike A N-D array of real values. Parameters: x(N,) arraylike A 1-D array of real values. The number of different x sample positions equals the number of different y sample positions. This class returns a function whose call method uses interpolation to find the value of new points.There's a third option, depending on how your (x,y,z) is set up. Method 3: No Interpolation (constraints on sampled data) This method produces the following graphs: Z = iddata((mat, mat), mat, (X,Y), method='nearest') # Depending on your "error", you may be able to use other methods # Interpolate (x,y,z) points over a normal (x,y) grid # This works if you have (x,y,z) tuples that you're *not* generating, and (x,y) points Method 2: Interpolating given z points over a regular grid # Method 2: Here, the returned matrix looks like: mat = , Y_err = (np.random.rand(*y.shape) - 0.5) * xy_max_error X_err = (np.random.rand(*x.shape) - 0.5) * xy_max_error # Half of this will be in the + direction, half will be in the - dir. # First we generate the (x,y,z) tuples to imitate "real" data First, I define a function that generates fake data: def gen_fake_data(): If you don't have that ability, and are given a fixed (x,y,z). This is relatively easy, since you can generate z at whatever points you want. # This works if you are generating z, given (x,y) # dim_? is the granularity in that direction
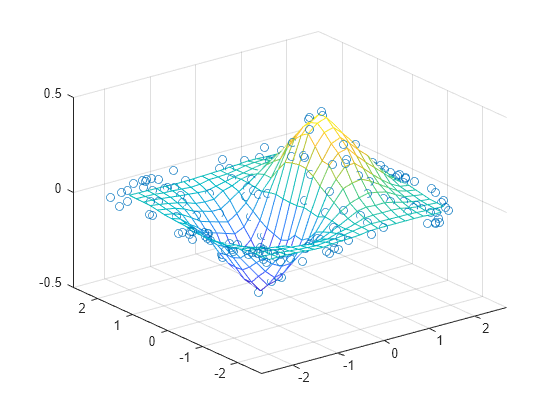
If you just have just a list of ( x, y, z) tuples, it's harder (see method_2() below, and maybe method_3()).Ĭonstants # min_? is minimum bound, max_? is maximum bound,

you know the formula for it) it's very easy (see method_1() below). Depending on whether you're generating z or not, you have at least two different options.


 0 kommentar(er)
0 kommentar(er)
